Prowise Learn
Spelend rekenen, taal en Engels oefenen in onze adaptieve software.
Probeer een maand gratisLeren met aandacht, waar elke leerling telt

Adaptief oefenen, op eigen niveau
Elke leerling leert op zijn of haar eigen manier en niveau. Met gebruik van AI-technologie worden de oefeningen afgestemd op het niveau van de leerling. De continuïteit waarmee dit gebeurt maakt Prowise Learn uitzonderlijk. Zo krijgt de leerling precies die uitdaging die nodig is. Het grote aantal behaalde successen houdt ze gemotiveerd.
- Continue meting van vaardigheden
- Direct aangepaste oefeningen
- Gekoppeld aan leerdoelen
- Altijd een succeservaring voor de leerling
Aan de slag met rekenen, taal en Engels
Verregaande adaptiviteit
Door de AI-technologie krijgt ieder kind de juiste uitdagingen.
Plezier voor ieder kind
Met stimulerende spellen en altijd succes blijft het leuk.
Inzicht in leerontwikkeling
Houd overzicht in het lerarendashboard zonder bewust te toetsen.
Eenvoudig te gebruiken
Maak een koppeling met Basispoort.
Ook als huiswerk
Thuis oefenen op de tablet, laptop of computer.

Zelfstandig rekenen met Rekentuin
Laat leerlingen aan de slag gaan met de basisbewerkingen en meer.
- Geschikt voor groep 1 t/m 8
- Spellen met klokkijken, tafels, breuken, verhaaltjessommen, geld en meer
- Gekoppeld aan leerdoelen
- Eindeloze oefeningen met bijna 70.000 rekensommen in 28 spellen

Taalzee: taal voor elk niveau
Op zoek naar extra oefenstof voor taal en spelling naast je huidige methode?
- Geschikt voor groep 1 t/m 8
- Woordenschat, zinsontleden, spelling, lezen, spreekwoorden, dictee en meer
- Gekoppeld aan leerdoelen
- Onbeperkt oefenen met 65.000 opgaven in 24 taalspellen

Engels oefenen met Words&Birds
Practice at your own level!
- Geschikt voor 8 t/m 14 jaar
- Oefenen met woordenschat, dictee, grammatica, spelling en Engelse uitdrukkingen
- Met audio-ondersteuning voor de juiste uitspraak
- Keuze uit ruim 25.000 opgaven in 13 spellen

Direct aan de slag met Prowise Learn
Wil je leerlingen op jouw school meteen laten oefenen met de oefenprogramma’s: Taalzee, Rekentuin of Words&Birds? Sluit dan vandaag nog een Prowise Learn abonnement af voor €4,- per leerling, per jaar.
Oefen je liever samen met je gezin thuis op de bank? Ontdek dan Prowise Learn voor families en sluit je abonnement af voor €50,- (5 licenties) per jaar.
Probeer Prowise Learn één maand gratis
Ontdek de wereld van Learn; alleen, met je collega’s of familie. Tijdens de proefmaand krijg je volledige toegang tot de spelomgeving en het leraren dashboard. Wil je liever alleen de spellen in Learn uitproberen? Vraag dan een gratis demo aan.

Continu in ontwikkeling met AI
Waarom het – met een Comenius-EduMedia-Award bekroonde – adaptieve meetsysteem van Prowise Learn relevant is voor de leerling van nu? Het intelligente meetsysteem wordt continu ontwikkeld met inzichten verkregen uit anonieme data.
Ook past Prowise Learn opgaven aan op basis van de vaardigheid van de leerling. Dit doen we met een innovatief, uniek systeem, ontwikkeld met AI-technologie. Geavanceerde algoritmen beoordelen leerlingen na elke gespeelde opgave en passen het aanbod daarop aan. Ook worden de opgaven na ieder antwoord beoordeeld en krijgen de leerlingen een aangepaste moeilijkheidsgraad. Hierdoor blijven zij oefenen met uitdagende maar haalbare oefeningen.
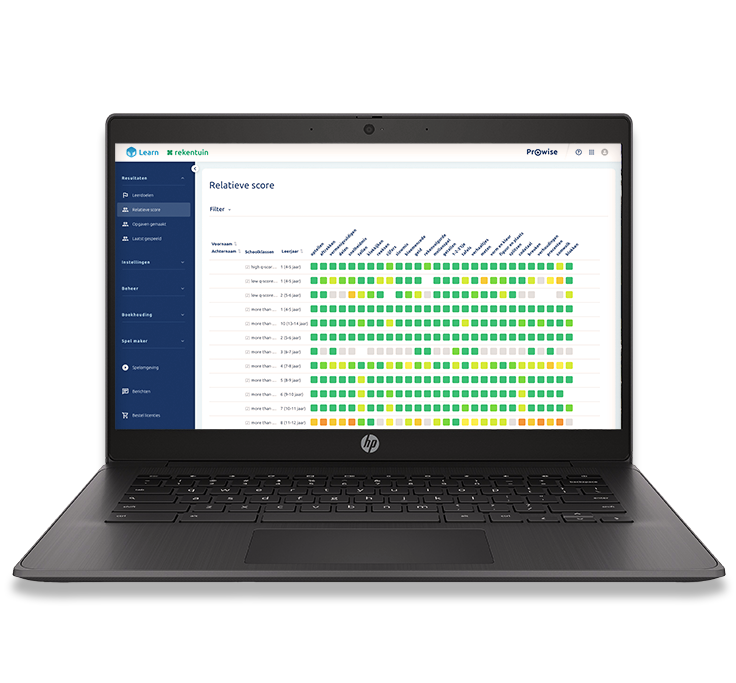
Volg de groei van je leerling
Krijg inzicht in de leerontwikkeling van je klas of van individuele leerlingen zonder te toetsen. Zo koppel je gemakkelijk persoonlijke leerdoelen in de oefenprogramma’s Rekentuin of Taalzee, en volg je de leerresultaten op de voet in het lerarendashboard. Of laat leerlingen zelf hun Groeikaart bekijken waarop hun scores en ontwikkelpunten staan.